正方形格子布局图片拖动的自动对齐功能

快速导航：

1、功能背景

2、功能要求

3、一般解决方案及问题

4、优化方案思路

5、代码实现

6、总结

功能背景

　　良无限首页的“魔方楼层”（也称百变楼层，图片按找格子大小制作，并可以自由布局图片顺序）是相当成功的页面展现形式，可以用非常有品质的形式，自由组合不同大小的banner或商品。这种布局方式出现后，曾被包括淘宝商城在内的多个页面或网站所借鉴。

　　这么有特色的楼层，维护上是个问题，一个比较好的方式，就是把魔方的每个元素用绝对定位排在楼层中，在后台做一个拖动图片的插件，让运营同学拖动图片到指定位置，并自动生成该元素的绝对定位的坐标。

　　图片拖动并不难实现，监测鼠标的移动即可。

　　然而，为了提高拖动的准确性，需要图片可以在一定范围内自动对齐到基准点的功能，这样运营同学可以更方便准确地排列图片。

　　这个“自动对齐”的功能虽然看起来很好实现，但是实现的方式未必都是最优的，现在让我们仔细瞧瞧这个看似简单的功能的实现思路。

功能要求

1、“魔方楼层”的每个格子的左上点坐标规定为基准点。

2、当图片被拖动到基准点周围的一定范围内（10px），图片自动对齐到基本点。

　　技术重点：判断当前坐标，是否在“基准点”的自动对齐范围内。

一般解决方案及问题

1、把所有“基准点”的坐标存储起来，图片每次移动时，都遍历“基准点库”，判断当前坐标是否在“基准点”的对齐范围之内。

2、“魔方”是由正方形组成，所以“基准点”之间是由规律的，所以优化上一个方案：“基准点库”其实可以自动生成，由 “width * n” 即可得出“基准点”， 再用一个上限（1000）来限制一下即可。

　　问题：以上方案都是基于“基准点库”、“遍历”、“对比”来实现的，我们会发现，遍历这个过程很难控制其效率，若再与每一次的鼠标移动监听的频率相叠加，这个实现貌似很笨重。那有没有更好的方式，脱离“基准点库”和“遍历”，只做简单的计算后进行对比就能实现呢？

优化方案思路

　　我优化的目的：脱离“基准点库”、“遍历”，只做简单的计算后进行对比。

　　所以，我的思路是，寻找“基准点”及“自动对齐范围”内的值的规律。

　　为了更好地描述这个方案，我们先明确、明确一下词汇表：

　　必要条件：

　　基准方格：组成“魔方”的基本单位，可以重复排列组成“魔方”，案例中的“基准方格”包括140×140的图片位+ 2px的图片间距，即142×142的方格。

　　基准边距（w）：“基准方格”边长，本例中是142

　　偏移量（e）：第一个“基准方格”的坐标，即“魔方”偏移（0,0）的偏移量，本例中是3.（横向纵向的偏移量必须相等。）

　　自动对齐范围（a）：“基准点”周围的一定距离，进入这个范围内，则对齐到“基准点”, 本例中是10，限制：a < w/2 （这个范围必须小于二分之一基准边距，如果大于，则不能判断将要靠近哪一个基准点）

　　当前坐标值（p）: 等待校验是否在“自动对齐范围”内的值 p = k + x

　　思路扩展：

　　基准点（k）：每个“基准方格”的左上顶点，但由于是正方形，所以“基准点”的“二维”的横纵坐标，可以简化为“一维”的方式。所以在本例中，“基准点”有：3、145、287、429、571、713、855，经过抽象，得出公式：k = w * n + e

　　基准点倍数（n）: 第几个基准点，n为整数，若n < 0，则代表 基准点为负值。

　　核心思路：“基准点”及“自动对齐范围”内的值的规律

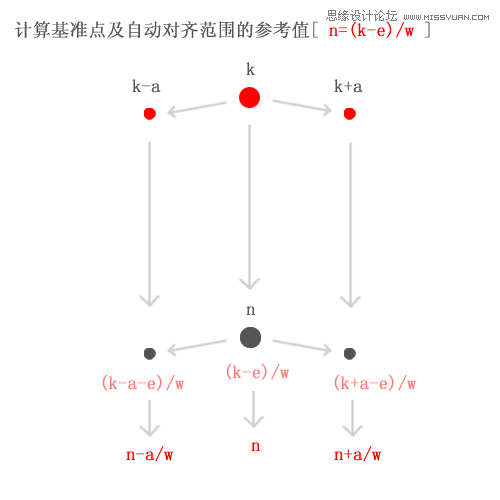
　　根据这个思路，我将“自动对齐范围”由 [ k-a , k+a ] 推导成为“参考范围”：[ n-a/w , n+a/w ]。

　　这样也可以有这个思路计算出来一个参考值，概念如下：

　　参考值（z）: “当前坐标值”经过一定运算得出的值，用来比较，以判断是否在“参考范围”内。计算方法：z = (p – e) / w

　　参考范围：自动对齐范围”的边界值，通过“参考值”的算法，得出的边界范围：[ n – a/w , n + a/w ]

　　如此一来，我只要通过把“当前坐标（p）”通过简单的计算 (p-e)/w，得出一个参考值(z)，再把这个参考值（z）,与他的参考边界（n-a/w  n+a/w）相比较，即可得出这个值是否在“自动对齐范围”之内的结论。

if(n-a/w <= (p-e)/w <= n+a/w){

//success

}

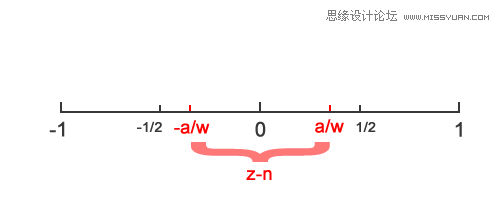
n-a/w <= z <= n+a/w

-a/w <= z – n <= a/w

由于 a < w/2 ，所以 a/w < 1/2 ，所以 |z-n| < 1/2，即：

这样的话貌似可以得出结论，但是遗憾的是n是不可知的，但是由|z-n| < a/w可以知道：

若 z > n ，则 z-n 在 [0, a/w]

若 z < n ，则 z-n 在 [-a/w, 0]

当 n > 0 时：

（z – z的整数位 = z的小数位）

若 z > n ，则 n = z的整数位 ；z-n = z的小数位 ；z的小数位在 [0, a/w]

若 z < n ，则 n-1 = z的整数位 ；z-(n-1) = z-n+1 = z的小数位 ；z的小数位在 [1-a/w, 1]

当 n = 0 时：

若 z > n ，则 n = z的整数位 ；z-n = z的小数位 ；z的小数位在 [0 , a/w]

若 z < n ，则 n = z的整数位 ；z-n = z的小数位 ；z的小数位在 [-a/w , 0] ；z的小数位的绝对值在 [0 , a/w]

(若 z < 0, 则整数位和小数位都小于0，如：(-4.25) – (-4) = -0.25）

当 n < 0 时：

若 z > n ，则 n+1 = z的整数位 ；z-(n+1) = z-n-1 = z的小数位 ；z的小数位在 [-1 , a/w-1] ；z的小数位的绝对值在 [1-a/w , 1]

若 z < n ，则 n = z的整数位 ；z-n = z的小数位 ；z的小数位在 [-a/w , 0] ；z的小数位的绝对值在 [0 , a/w]

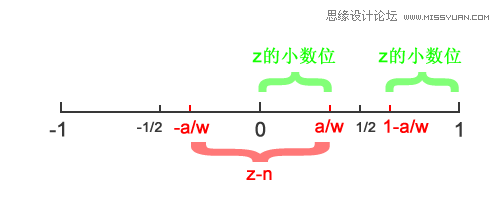
综上所述：

z的小数位的绝对值 在 [0 , a/w] 或 [1-a/w , 1]

即：

这样一来，只要通过z = (p-e)/w计算出z的值，取出小数位，然后在[0 , a/w]、[1-a/w , 1]区间中比较，就可以得出结论了。

代码实现

　　好，接下来分享一下如何实现以上方案：

1、输入和输出：

输入：当前坐标数值、基准边距、偏移量（默认为0）、自动靠近范围（默认为10）

输出：当前坐标值是否在自动对齐范围内（boolean）、目标坐标数值

2、具体代码：

/**
* isPos 正方形格子布局的自动对齐
* @description 在正方形格子布局的自动对齐中，用于判断当前位置是否进入自动对齐范围，并返回目标位置
* @param {Object} config 配置项
* @param {Number} config.pos 当前坐标数值（横坐标或纵坐标） 必填
* @param {Number} config.standard 标准边长 必填
* @param {Number} [config.offset] 偏移量 默认为0
* @param {Number} [config.autoRang] 自动对齐范围 默认为10
* @return {Object} obj 返回对象
* @return {Boolean} obj.status 当前坐标值是否在自动对齐范围内
* @return {Number} obj.pos 目标坐标值
* @example
* //配置示例
* var config = {
*    pos: 156,
*    standard: 142,
*    offset: 3,
*    autoRang: 10
* };
*/
var isPos = function(config){
    var pos = parseInt(config.pos, 10),
        standard = parseInt(config.standard, 10),
        offset = parseInt(config.offset, 10) || 0,
        autoRang = parseInt(config.autoRang, 10) || 10,
        fixed = parseInt(config.fixed, 10) || 3,
        targetPos = pos,
        posStatus = false,
        r1, r2, referPos, n;
    
    if((!pos && pos != 0) || !standard) return {};

    /**
    * 计算坐标值的参考值(与标准边长相除)
    */
    var getReferPos = function(_pos){
        var z = parseFloat((_pos/standard).toFixed(fixed)),
            int = parseInt(z, 10);
        return {
            z: z,
            int: int,
            float: Math.abs(parseFloat((z - int).toFixed(fixed)))
        };
    }(pos - offset);

    n = getReferPos.int;
    referPos = getReferPos.float;
    r2 = parseFloat((autoRang/standard).toFixed(fixed));
    r1 = 1 - r2;

    if((referPos >= r1 && referPos <= 1) || (referPos <= r2 && referPos >= 0)){
        n = (referPos >= r1 && referPos <=1) ? (getReferPos.z > 0 ? n+1 : n-1) : n;
        //计算自动靠齐的目标位置。
        targetPos = n * standard + offset;
        posStatus = true;
    }

    return {
        status: posStatus,
        pos: targetPos,
        z: getReferPos.z,
        n: n,
        r: referPos
    };
};

3、DEMO与测试：

http://lp.taobao.com/go/act/lptest/ispostest.php

总结

　　这个小功能看似很不起眼，但是经过分析及抽象，不仅通过巧妙的算法解决了性能问题，还抽象出来以后解决类似问题的通用方法。

　　上述算法，可用于格子的布局中，格子可以是长方形，格子数目没有限制，偏移量没有限制、格子大小也没有限制。不用遍历基准点库，只通过简单计算及比较，即可得出是否需要自动对齐的结果。算法相对精炼。

　　问题虽小，但是精益求精的解决问题，是我们所追求的。

　　最后分享 几句话，是TMS标题中的：

　　生活中的万事万物，无不可以吸收教益，无不可以成文，只要“求思之深而无不在”定能有所得益。

　　知识需要反复探索，土地需要辛勤耕耘。

　　最后，感谢夏达同学帮这篇文章设计的主题图片，非常有品质感！